Reinforcement Learning
Table of Contents
Reinforcement learning (RL) (Sutton, 1998) is all about the interaction between an agent and its environment, where learning occurs through trial-and-error. The agent observes the current state of the environment, takes actions based on these observations, and influences new possible state configurations while receiving rewards based on its actions. The primary objective is to maximize cumulative rewards, which drives the agent’s sequence of decisions towards achieving specific goals, such as escaping from a maze, winning an Atari (Mnih. 2013) , or defeating the world champion of Go (Silver, 2016). But how does the agent learn to act effectively to achieve its goal? RL algorithms are designed to maximize the total rewards obtained by the agent, thereby guiding its actions towards these objectives.
In this post, we will introduce the essential concepts of RL required to implement these agents. We will specifically focus on model-free RL, where the agent learns to act without constructing a model of its environment, as opposed to model-based RL, which involves such modeling. The goal is to design agents that learn to perform well solely by consuming experiences from their environment. By understanding the fundamentals of designing such agents, we will explore policy optimization methods, such as REINFORCE and PPO, which are used to refine the agent’s behavior.
With the knowledge gained from this chapter, we will be equipped to set-up and implement this framework under popular research environment such as ATARI pong.
The Framework for Learning to Act
The starting point for designing agents that learn to act is the Markov Decision Process (MDP) framework \cite{Sutton1998}. An MDP is a mathematical object that describes the interaction between the agent and the environment. This interaction is characterized by a tuple , where:
- , state space, set of possible states in the environment.
- , action space, set of possible actions available to the agent.
- , transition probability distribution, which gives the probability of the environment for transitioning to a new state with a reward given the current state and action .
- , reward function, which provides a scalar feedback signal (aka reward) to the agent after taking an action and reaching the subsequent state .
- , **initial state distribution**, which determines the probability of the agent starting in a particular state.
- is the discount factor, which determines the importance of future rewards.
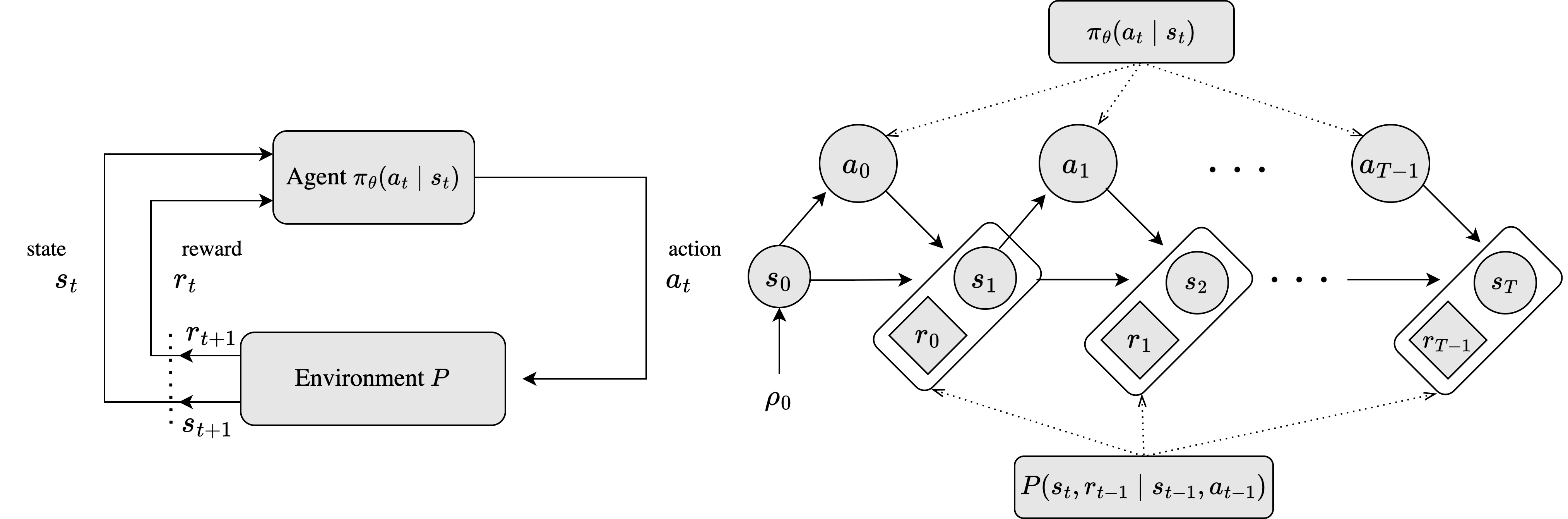
Figure 1. Left: A loop representation of a Markov Decision Process (MDP). Right: An unrilled MDP depecting an episodic case with a finite horizon \\(T\\) and a parameterized policy \\(\pi\_{\theta}\\).
Markov Decision Processes generate sequences of state-action pairs, or trajectories , starting from an initial state . The agent’s behavior is determined by a policy , which maps states to a probability distribution over actions. An action is chosen, leading to the next state according to the transition distribution , and a reward is received. This cycle repeats iteratively, with the agent selecting actions, transitioning through states, and receiving rewards, as shown on the left side of Figure 1. Thus, the trajectory encapsulates the dynamic sequence of state-action pairs resulting from the agent’s interaction with its environment.
The process can continue indefinitely, known as an infinite horizon, or be confined to episodes that end in the terminal state , referred to as episodic tasks, such as winning or losing a game, as illustrated on the right side of Figure 1. It is important to note that the transition to the next state depends only on the current state and action, not on the sequence of prior events. This characteristic is known as the _Markov property_, which states that the future and the past are conditionally independent, given the present (_memoryless_). In this work, we focus on the episodic setting, where the trajectory begins at and concludes at , with a finite horizon . Therefore, the trajectory is defined as , summarizing the agent’s behavior throughout the episodic task.
In reinforcement learning, the primary goal is for the agent to develop a behavior that maximizes the expected return from its actions results within the environment. This concept of maximization is formalized through the objective function , which aims to maximize the expected return over a collection of trajectories generated by the policy , commonly referred to as “policy rollouts”. The term “rollout” is used to describe the process of simulating the agent’s behavior in the environment by executing the policy and observing the resulting trajectory . The objective function is defined as follows:
The return over a trajectory is defined as the accumulated discounted rewards of the trajectory, . The reward signals are the inmmediate effect of taking the actions, and the return is the cumulative rewards obtained during the trajectory, considering a discount factor , which gives more importance to the rewards of nearer actions than to future rewards.
Policy Optimization
In reinforcement learning there are different approaches to solve the MDP formulated in the previous section, which are summarized in Figure 2. The most common are value-based methods and policy-based methods. In value-based methods, the agent learns which state is more valuable and take action that leads to it. In policy-based methods, the agent learns a policy that directly maps states to actions. In this work we will focus on the latter methods, specifically in policy gradients.
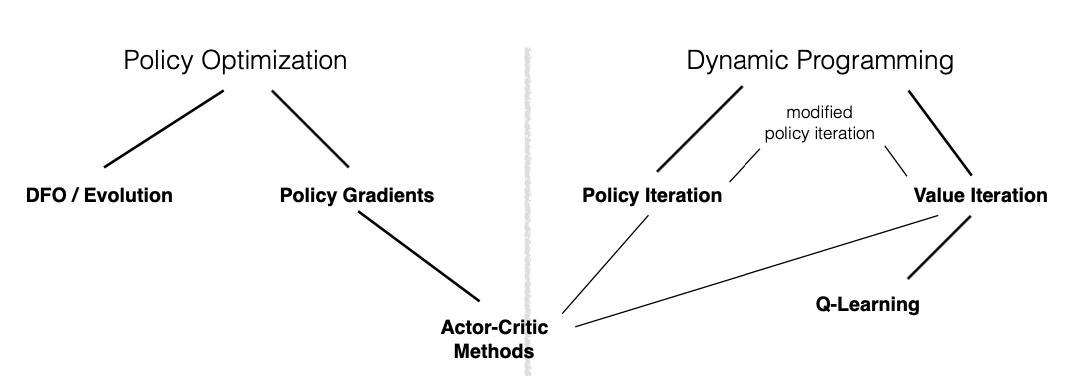
Other approaches for finding a policy is by non solving the MDP, but by directly optimizing the policy. This is the case of derivative free optimization (DFO), or evolutionary algorithms, in which the policy is parameterized by a vector , and the agent explores the space of parameters by searching. Nothing of the temporal structure and actions of the MDPs are considered in this kind of solution.
Policy gradient methods provide a way to reduce reinforcement learning to stochastic gradient descent, by providing a connection between how function approximation is solved in supervised learning settings, but with the key diffrence that the dataset is collected using the model itself plus a reward signal that acts as a “label”.
Learning the Policy
The starting point is to think of trajectories as units of learning instead of individual observations (i.e., actions). What dynamics generate a trajectory? Given a policy , represented as a function with parameter , whose input is a representation of the state and whose output is action selection probabilities, we can deploy the agent into its environment at an initial state and observe its actions in inference mode or _evaluation phase_ \citep{sutton1999policy}. The agent continuously promotes actions based on the current state until the episode ends in a terminal state, when . At this point, we can determine if the goal was accomplished, such as winning the ATARI Pong game, or generating aesthetically pleasing samples from a diffusion model. The returns are the scalar value that assets perfomance whether we have achieved the ultimate goal, effectively acting as a “proxy” of a label for the overall trajectory. Thus, the trajectory serves as our unit of learning, and the remaining task is to establish the feedback mechanism for the _learning phase_.
Intuitivelly, we want to collect the trajectories and make the good trajectories and actions more probable, and push the actions towards betters actions.
Mathematically, we aim to perform stochastic optimization to learn the agent’s parameters. This involves obtaining gradient information from sample trajectories, with performance assessed by a scalar-value function (i.e. reward). The optimization is stochastic because both the agent and the environment contain elements of randomness, meaning we can only compute estimates of the gradient. Crucially, we are estimating the gradient of the expected return with respect to the policy parameters. To address this, we employ Monte Carlo Gradient Estimation \citep{mohamed2020monte}, specifically using the score function method. From a machine learning perspective, this involves dealing with the stochasticity of the gradient estimates, , and using gradient ascent algorithms to update the policy parameters based on these estimates, along with a learning rate to control the step size of the optimization process,
Gradient Estimation via Score Function
The gradient estimation can be obtained using the score function gradient estimator. Let’s introduce the following probability objective , defined in the ambient space and with parameters ,
Here, is a scalar-valued function, similar to how the reward is represented in the reinforcement learning setting. The score function is the derivative of the log probability distribution with respect to its parameters . We can use the following identity to establish a connection between the score function and the probability distribution ,
Therefore, taking the gradient of the objective with respect to the parameter , we have
The use of the log-derivative rule on the above equation to introduce the score function is also known as the log-derivative trick. Now, we can compute an estimate of the gradient, , using Monte Carlo estimation with samples from the distribution as follows:
We draw samples , compute the gradient of the log-probability for each sample, and multiply by the scalar-valued function evaluated at the sample. The average of these terms is an unbiased estimate of the gradient of the objective , which we can use for gradient ascent.
There are two important points to mention about the previous equation.
- The function can be any arbitrary function we can evaluate on . Even if is non-differentiable with respect to , it can still be used to compute the gradient estimation .
- The expectation of the score function is zero, meaning that the gradient estimator is unbiased
The last point is particularly useful because we can replace with a shifted version given a constant , and still obtain an unbiased estimate of the gradient, which can be beneficial for the optimization task:
Using a baseline function to determine , that does not depend on the parameter , can reduce the variance of the estimator \citep{mohamed2020monte}. The baseline function, which satisfies the property that the score function expectation is zero, can be any function independent of . When a baseline is chosen to be close to the scalar-valued function , it effectively reduces the variance of the estimator. This reduction in variance helps stabilize the updates by minimizing fluctuations in the gradients estimates, leading to more reliable and efficient learning.
Vanilla Policy Gradient, aka REINFORCE
The REINFORCE algorithm \citep{williams1992simple} translates the previous derivation of gradient estimation via the score function into reinforcement learning terminology. This is the earliest member of the Policy Gradient family (Figure~), where the objective is to maximize the expected return of the trajectory under a policy parameterized by (e.g., a neural network). At each state , the agent takes an action according to the policy , which generates a probability distribution over actions . Here, we will use the notation instead of .
As we mentioned in previous section, a trajectory represents the sequence of state-action pairs resulting from the agent’s interaction with its environment. From the initial state to the terminal state , the trajectory is a sequence of states and actions, , which describes how the agent acts during the episodic task. Let be the probability of obtaining the trajectory under the policy .
We thus have a distribution of trajectories. Remember that the trajectory is the learning unit for our policy , as it tells us if the consequences of each action led to a favorable final outcome on the terminal state (e.g. win/lose). The goal is to maximize the exptected return of the trajectories on average, and the return could be the cumulative rewards obtained during the ***episode*** or the discounted rewards. The expected return is given by the following expression:
This is the objective we want to maximize, which is a particular case of Equation~() with the scalar-valued function , representing the return of the trajectory. Let’s use the techniques from the previous section to compute the gradient of the objective in Equation~() with respect to the policy parameter . The gradient estimation is given by:
What is exactly? Given that the trajectory is a sequence of states and actions, and assuming the Markov property imposed by the MDP, the probability of the trajectory is defined as follows:
In the above expression, denotes the distribution of initial states, while represents the transition model, which updates the environment context based on the action taken in the current state . A crucial step in estimating the gradient is computing the logarithm of the trajectory probability. Following this, we calculate the gradient with respect to the policy parameter ,
The distribution of initial states and the transition probabilities are disregarded because they are independent of , thereby simplifying significantly the computations needed for gradient estimation. By substituting the final expression from Equation~() into the gradient estimation of the objective in Equation~(\ref {eqn:rl-gradient-estimator-vanilla}), we derive the REINFORCE gradient estimator
The core concept is to collect a set of trajectories under the policy and update the policy parameters to increase the likelihood of high-reward trajectories while decreasing the likelihood of low-reward ones, as illustrated in Figure~. This trial-and-error learning approach, described in Algorithm 1, repeats this process over multiple iterations, reinforcing successful trajectories and discouraging unsuccessful ones, thus encoding the agent’s behavior in its parameters.
- Initialize policy , set learning rate
- For :
- Collect a set of trajectories by sampling from the current policy
- Calculate the returns for each trajectory
- Update the policy:
Reducing the variance of the estimator. Using two techniques, reward-to-go and baseline, we can improve the quality of the gradient estimator in Equation~().
The reward-to-go technique is a simple trick that can reduce the variance of the gradient estimator by taking advantage of the temporal structure of the problem. The idea is to weight the gradient of the log-probability of an action by the sum of rewards from the current timestep to the end of the trajectory . This way, the gradient of the log-probability of an action is only weighted by the consequence of that action on the future rewards, removing terms that do not depend on . Let’s introduce this technique by using the gradient estimation in Equation~() and replacing naively using the sum of total trajectory reward **\footnote**{The same applies for discounted returns or other kind of returns .}
As we saw at the end of Section~, it is possible to reduce the variance of the gradient estimator by using a baseline function, , without biasing the estimator. However, is the expectation of the score still unbiased in this setting?
The proof follows a similar argument as shown in Equation~(), with the key difference being that the expectation is taken with respect , which is a sequence of random variables. By leveraging the linearity of the expectation property, we can focus on a single term at step of Equation~() to demonstrate that the baseline does not affect the expectation of the score function. We split the trajectory sequence at step into: and , and then expand it into state-action pairs **\footnote**{A criterion used when splitting the trajectory is that state-action pairs are formed given that is a consequence of action , and taking action results in state . Notice both expectations from step 1 and 2 in Equation~().}
We can remove irrelevant variables from the expectation over the portion of the trajectory because we are focusing on the term at step . The only relevant variable is , and the expectation is 1. Given that the gradient with respect to of a constant is zero, and is multiplying it, the effect of the baseline on the expectation is nullified. This argument can be applied to any other term in the sequence due to the linearity of the expectation. Therefore, we have proven that using a baseline also keeps the gradient estimator unbiased in the policy gradient setting.
Choosing an appropriate baseline is a critical decision in reinforcement learning \citep{foundations-deeprl-series-l3}, as different methods can offer unique strengths and limitations. Common baselines include fixed values, moving averages, and learned value functions.
- Constant baseline: .
- Optimal constant baseline: .
- Time-dependent baseline: .
- State-dependent expected return: .
The control variates method can significantly reduce estimator variance, enhancing the stability and performance of RL algorithms \cite{NIPS2001_584b98aa}. Despite the nuances and differences among baseline methods, the primary concept is the advantage, shown in Equation~(), which refers to increase log probabilities of action proportionally to how much its returns, , are better than the expected return under the current policy, which is determined by the value function
What remains is how do we get estimates for in practice.
Actor-Critic Methods
Actor-Critic referred to learn concurrently models for the policy and the value function. This methods are more data efficient because they amortize the samples collected used for Monte Carlo estimations while reducing the variance of the gradient estimator. The actor controls how the agent behaves—by updating the policy parameters as we see in previous sections—whereas the critic measures how good the taken action is, and could be a state-value () or action-value () \footnote{Action-value function () refers to the value of take action on state under a policy .} function. Notice that we are combining in some way both approaches for solving MDPs as is depicted in Figure~.
We are introducing a new function approximator for the value function, , where are the parameters of the value function
The objective is to minimize the mean squared error (MSE) between the estimated value and the empirical return, i.e. we are regress the value against empirical return in a supervised learning fashion
Algorithm 2 describes the steps for a REINFORCE variant with advantage , which combines the actor-critic approach with the traditioinoal REINFORCE algorithm. More components were introduced and can influence in the performance when the algorithm is implemented. For instance, the policy and value networks can share parameters or not. A useful study that make abalations and suggestions to pay attention when these algorithms are implemented is What Matters In On-Policy Reinforcement Learning? A Large-Scale Empirical Study (Andrychowicz, 2020 \cite{andrychowicz2020mattersonpolicyreinforcementlearning}).
- Initialize policy
- Initialize value
- Set learning rates and
- For :
- Collect a set of trajectories by sampling from the current policy
- Calculate the returns for each trajectory
- Update the policy:
- Update the value:
References
[1] Sutton, R. S. (2018). Reinforcement learning: An introduction. A Bradford Book.
[2] Mnih, V. (2013). Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602.
[3] Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., ... & Hassabis, D. (2017). Mastering the game of go without human knowledge. nature, 550(7676), 354-359.
[4] Schulman, J. (2016). Optimizing expectations: From deep reinforcement learning to stochastic computation graphs (Doctoral dissertation, UC Berkeley).